Trong lĩnh vực khoa học máy tính, thuật toán sắp xếp là một phần quan trọng của việc xử lý dữ liệu. Có nhiều thuật toán sắp xếp khác nhau, mỗi thuật toán có ưu điểm và hạn chế riêng. Trong bài viết này, chúng ta cùng nhau thảo luận và tìm hiểu về thuật toán sắp xếp nổi bọt (Bubble Sort) - một thuật toán đơn giản và dễ hiểu. Chúng ta sẽ khám phá cách thuật toán này hoạt động, phân tích độ phức tạp và xem xét ưu nhược điểm cũng như ứng dụng của nó.
Khái niệm thuật toán sắp xếp nổi bọt
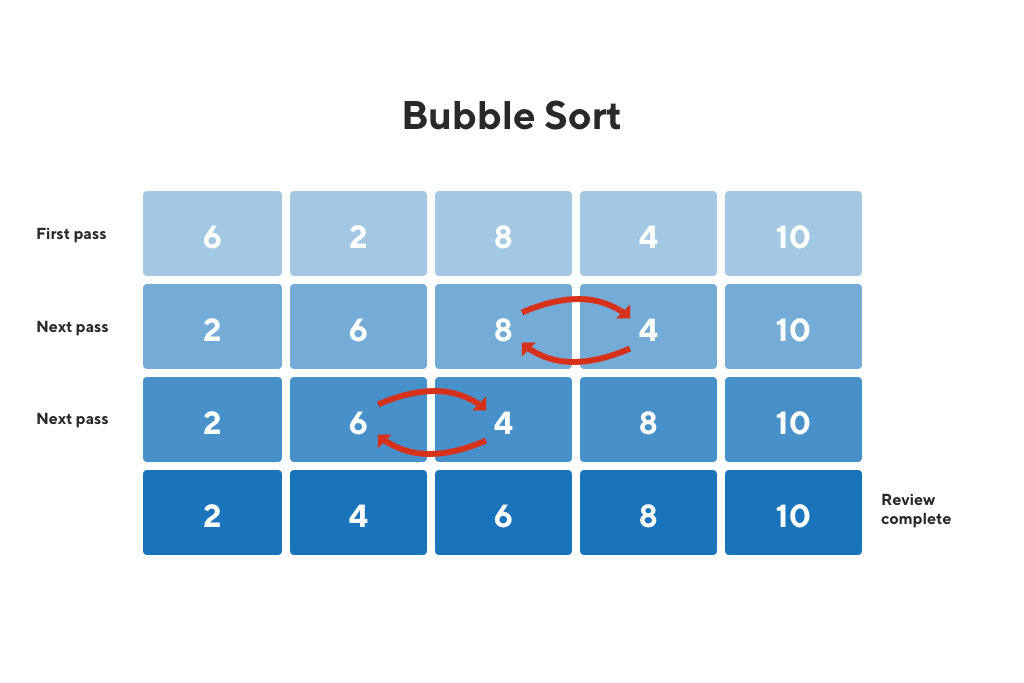
Sắp xếp nổi bọt (tiếng Anh: Bubble Sort) là một thuật toán sắp xếp lấy cảm hứng từ các bọt nước nổi lên trên mặt nước. Nó là thuật toán được thiết kế để sắp xếp một danh sách dữ liệu theo thứ tự tăng dần hoặc giảm dần bằng cách so sánh cặp phần tử liền kề và hoán đổi chúng nếu chúng không theo thứ tự mong muốn. Quá trình này tiếp tục cho đến khi không còn cặp phần tử nào cần hoán đổi nữa, tức là danh sách đã được sắp xếp theo thứ tự mong muốn.
Cách thức hoạt động của thuật toán sắp xếp nổi bọt
Thuật toán sắp xếp nổi bọt hoạt động theo các bước sau:
- Bước 1: Bắt đầu từ đầu danh sách, so sánh phần tử đầu tiên với phần tử thứ hai. Nếu phần tử đầu tiên lớn hơn phần tử thứ hai (hoặc nhỏ hơn nếu thứ tự mong muốn là giảm dần) thì hoán đổi chúng. Nếu không, giữ nguyên vị trí ban đầu.
- Bước 2: Tiếp tục quá trình trên, so sánh phần tử thứ hai với phần tử thứ ba. Lặp lại quá trình này cho đến khi ta so sánh phần tử thứ lần lượt với phần tử thứ cuối cùng.
- Bước 3: Khi hoàn thành vòng lặp đầu tiên, phần tử lớn nhất trong danh sách sẽ được đặt ở vị trí cuối cùng.
- Bước 4: Lặp lại các bước trên cho đến khi không còn cần hoán đổi nữa. Quá trình sẽ kết thúc khi danh sách đã được sắp xếp theo thứ tự tăng dần.
Giả sử ta có mảng arr = {16, 22, 20, 24, 12, 6} và ta muốn sắp xếp theo thứ tự tăng dần, thì thực hiện thuật toán như sau:
- Bắt đầu với cặp đầu tiên là hai phần tử đầu của mảng, ta sẽ hoán đổi hai phần tử này cho nhau nếu phần tử đầu tiên lớn hơn phần tử thứ hai. Vì 16 < 22 nên ta giữ nguyên hai phần tử này và chuyển sang cặp tiếp theo.
- Cặp tiếp theo là 22 và 20. Ta làm tương tự như trên, vì 22 > 20 nên ta sẽ hoán đổi hai phần tử này cho nhau.
- Qua cặp 22 và 24, vì 22 < 24 nên ta không cần phải hoán đổi.
- Tới cặp 24 và 12. Vì 24 > 12 nên ta hoán đổi hai phần tử này.
- Tới cặp cuối cùng là 24 và 6. Vì 24 > 6 nên ta hoán đổi hai phần tử này cho nhau.
- Sau khi lặp hết tất cả các cặp, ta đã đưa 24 là số lớn nhất của mảng ra vị trí đúng nằm ở cuối mảng. Như vậy 24 được coi là đã được sắp xếp, và ta sẽ quay về lại từ đầu, lặp lại các bước trên với phần còn lại. Cặp đầu tiên là 16 và 20, vì 16 < 20 nên ta giữ nguyên hai phần tử này.
- Tương tự như vậy, vì 20 < 22 nên ta vẫn giữ nguyên.
- Qua cặp tiếp theo, vì 22 > 12 nên ta đổi vị trí hai phần tử này cho nhau.
- Tương tự, vì 22 > 6 nên ta tiếp tục hoán đổi hai phần tử này.
- Vì 24 đã được sắp xếp nên ta sẽ bỏ qua và không quan tâm đến nó. Vậy coi như phần tử tiếp theo là 22 đã ở đúng vị trí, ta sẽ quay lại cặp đầu tiên là 16 và 20. Vì 16 < 20 nên ta giữ nguyên hai phần tử này.
- Qua cặp tiếp theo, vì 20 > 12 nên ta sẽ hoán đổi hai phần tử này.
- Tương tự như vậy, vì 20 > 6 nên ta tiếp tục tráo vị trí hai phần tử cho nhau.
- Sau đó ta quay về cặp đầu tiên, vì 16 > 12 nên ta sẽ tráo hai phần tử này.
- Tương tự, ta lại tráo 16 và 6 cho nhau vì 16 > 6.
- Quay lại cặp đầu tiên, vì 12 > 6 nên ta hoán đổi hai phần tử này với nhau.
- Như vậy không còn cặp phần tử nào cần so sánh. Ta kết luận mảng đã được sắp xếp hoàn toàn với thứ tự mong muốn.
Triển khai thuật toán
Sau đây là code triển khai thuật toán sắp xếp nổi bọt bằng những ngôn ngữ khác nhau mà bạn có thể tham khảo.
C
#include <stdio.h>// Hàm xuất mảngvoid printArr(int arr[], int arrLength){for (int i = 0; i < arrLength; i++){printf("%d ", arr[i]);}printf("\n");}// Hàm sắp xếpvoid bubbleSort(int arr[], int arrLength){// Lặp qua mảng arr, i cũng đại diện cho số phần tử đã được đưa về vị trí đúngfor (int i = 0; i < arrLength; i++){// Vòng lặp for lồng để so sánh các cặp phần tử, bỏ qua i phần tử đã được sắp xếpfor (int j = 0; j < arrLength - 1 - i; j++){// Nếu phần tử tại vị trí j lớn hơn phần tử tại vị trí kề phải thì hoán đổi hai phần tử cho nhauif (arr[j] > arr[j + 1]){int temp = arr[j];arr[j] = arr[j + 1];arr[j + 1] = temp;}}}}int main(int argc, char const *argv[]){int arr[] = {16, 22, 20, 24, 12, 6};int arrLength = sizeof(arr) / sizeof(arr[0]);printf("Mang ban dau: ");printArr(arr, arrLength);bubbleSort(arr, arrLength);printf("Mang da duoc sap xep: ");printArr(arr, arrLength);return 0;}
C++
#include <iostream>using namespace std;// Hàm xuất mảngvoid printArr(int arr[], int arrLength){for (int i = 0; i < arrLength; i++){cout << arr[i] << " ";}cout << endl;}// Hàm sắp xếpvoid bubbleSort(int arr[], int arrLength){// Lặp qua mảng arr, i cũng đại diện cho số phần tử đã được đưa về vị trí đúngfor (int i = 0; i < arrLength; i++){// Vòng lặp for lồng để so sánh các cặp phần tử, bỏ qua i phần tử đã được sắp xếpfor (int j = 0; j < arrLength - 1 - i; j++){// Nếu phần tử tại vị trí j lớn hơn phần tử tại vị trí kề phải thì hoán đổi hai phần tử cho nhauif (arr[j] > arr[j + 1]){int temp = arr[j];arr[j] = arr[j + 1];arr[j + 1] = temp;}}}}int main(int argc, char const *argv[]){int arr[] = {16, 22, 20, 24, 12, 6};int arrLength = sizeof(arr) / sizeof(arr[0]);cout << "Mang ban dau: ";printArr(arr, arrLength);bubbleSort(arr, arrLength);cout << "Mang da duoc sap xep: ";printArr(arr, arrLength);return 0;}
C#
using System;namespace Main{class Program{// Phương thức xuất mảngstatic void printArr(int[] arr){foreach (int i in arr){Console.Write($"{i} ");}Console.WriteLine();}// Phương thức sắp xếpstatic void bubbleSort(int[] arr){// Lặp qua mảng arr, i cũng đại diện cho số phần tử đã được đưa về vị trí đúngfor (int i = 0; i < arr.Length; i++){// Vòng lặp for lồng để so sánh các cặp phần tử, bỏ qua i phần tử đã được sắp xếpfor (int j = 0; j < arr.Length - 1 - i; j++){// Nếu phần tử tại vị trí j lớn hơn phần tử tại vị trí kề phải thì hoán đổi hai phần tử cho nhauif (arr[j] > arr[j + 1]){int temp = arr[j];arr[j] = arr[j + 1];arr[j + 1] = temp;}}}}static void Main(){int[] arr = {16, 22, 20, 24, 12, 6};Console.Write("Mang ban dau: ");printArr(arr);bubbleSort(arr);Console.Write("Mang da duoc sap xep: ");printArr(arr);}}}
Java
import java.util.Arrays;public class Main {// Phương thức sắp xếppublic static void bubbleSort(int[] arr) {// Lặp qua mảng arr, i cũng đại diện cho số phần tử đã được đưa về vị trí đúngfor (int i = 0; i < arr.length; i++) {// Vòng lặp for lồng để so sánh các cặp phần tử, bỏ qua i phần tử đã được sắp xếpfor (int j = 0; j < arr.length - 1 - i; j++) {// Nếu phần tử tại vị trí j lớn hơn phần tử tại vị trí kề phải thì hoán đổi hai phần tử cho nhauif (arr[j] > arr[j + 1]) {int temp = arr[j];arr[j] = arr[j + 1];arr[j + 1] = temp;}}}}public static void main(String[] args) {int[] arr = {16, 22, 20, 24, 12, 6};System.out.println("Mang ban dau: " + Arrays.toString(arr));bubbleSort(arr);System.out.println("Mang da duoc sap xep: " + Arrays.toString(arr));}}
Python
# Hàm sắp xếpdef bubbleSort(lst):# Lặp qua danh sách lst, i cũng đại diện cho số phần tử đã được đưa về vị trí đúngfor i in range(len(lst)):# Vòng lặp for lồng để so sánh các cặp phần tử, bỏ qua i phần tử đã được sắp xếpfor j in range(len(lst) - 1 - i):# Nếu phần tử tại vị trí j lớn hơn phần tử tại vị trí kề phải thì hoán đổi hai phần tử cho nhauif lst[j] > lst[j + 1]:lst[j], lst[j + 1] = lst[j + 1], lst[j]lst = [16, 22, 20, 24, 12, 6]print(f"Danh sách ban đầu: {lst}")bubbleSort(lst)print(f"Danh sách đã được sắp xếp: {lst}")
JavaScript
// Hàm sắp xếpfunction bubbleSort(arr) {// Lặp qua mảng arr, i cũng đại diện cho số phần tử đã được đưa về vị trí đúngfor (let i = 0; i < arr.length; i++) {// Vòng lặp for lồng để so sánh các cặp phần tử, bỏ qua i phần tử đã được sắp xếpfor (let j = 0; j < arr.length - 1 - i; j++) {// Nếu phần tử tại vị trí j lớn hơn phần tử tại vị trí kề phải thì hoán đổi hai phần tử cho nhauif (arr[j] > arr[j + 1]) {let temp = arr[j];arr[j] = arr[j + 1];arr[j + 1] = temp;}}}}let arr = [16, 22, 20, 24, 12, 6];window.alert("Mảng ban đầu: " + arr);bubbleSort(arr);window.alert("Mảng đã được sắp xếp: " + arr);
Phân tích độ phức tạp về thời gian và bộ nhớ
Độ phức tạp về thời gian
Trong trường hợp xấu nhất, khi danh sách đã được sắp xếp theo thứ tự ngược lại, thuật toán sắp xếp nổi bọt sẽ có độ phức tạp O(n^2), với n là số lượng phần tử trong danh sách. Trong trường hợp tốt nhất, khi danh sách đã được sắp xếp theo thứ tự mong muốn, thuật toán sắp xếp nổi bọt có độ phức tạp O(n), với n là số lượng phần tử trong danh sách.
Độ phức tạp về bộ nhớ
Thuật toán sắp xếp nổi bọt chỉ sử dụng một hằng số lượng bộ nhớ bổ sung để lưu trữ các biến tạm thời và chỉnh sửa giá trị của chúng. Do đó, độ phức tạp về bộ nhớ của thuật toán này là O(1).
Ưu điểm và hạn chế của thuật toán sắp xếp nổi bọt
Ưu điểm
- Dễ hiểu và cài đặt: Thuật toán sắp xếp nổi bọt là một thuật toán đơn giản và dễ hiểu, không đòi hỏi kiến thức toán học phức tạp. Việc cài đặt thuật toán cũng rất đơn giản và không tốn nhiều công sức.
- Ổn định: Thuật toán sắp xếp nổi bọt có tính ổn định vì nó luôn đảm bảo được thứ tự của các phần tử cùng giá trị trong danh sách cần sắp xếp
- Không yêu cầu thêm bộ nhớ phụ: Như đã phân tích độ phức tạp về bộ nhớ ở trên, thuật toán sắp xếp nổi bọt chỉ sử dụng một lượng bộ nhớ hằng số là O(1), không tạo thêm gánh nặng cho hệ thống.
Hạn chế
Tuy thuật toán có những ưu điểm nói trên, nó có một hạn chế đáng chú ý như sau:
- Kém hiệu quả với danh sách lớn: Như đã phân tích trên, thuật toán sắp xếp nổi bọt có độ phức tạp O(n^2), điều này làm cho thuật toán này kém hiệu quả so với các thuật toán sắp xếp khác như sắp xếp nhanh (Quick Sort) hoặc sắp xếp trộn (Merge Sort).
- Không hiệu quả với danh sách gần như đã được sắp xếp: Khi danh sách gần như đã sắp xếp, thuật toán sắp xếp nổi bọt vẫn phải thực hiện nhiều thao tác so sánh và hoán đổi, dẫn đến sự lãng phí thời gian.
Ứng dụng
Mặc dù Bubble Sort không được sử dụng rộng rãi trong các ứng dụng thực tế, nhưng vì tính đơn giản của nó, nó vẫn có thể được sử dụng trong các tình huống sau:
- Sắp xếp các danh sách nhỏ: Khi ta có các danh sách có số lượng phần tử nhỏ, Bubble Sort có thể được áp dụng một cách hiệu quả và dễ dàng.
- Mục đích giảng dạy: Vì tính đơn giản và dễ hiểu, Bubble Sort thường được sử dụng trong quá trình giảng dạy lập trình và thuật toán để giúp người học hiểu rõ về cách hoạt động của thuật toán sắp xếp.
Kết
Trong tổng quan, thuật toán sắp xếp nổi bọt là một thuật toán sắp xếp đơn giản và dễ hiểu. Mặc dù có nhược điểm về độ phức tạp và hiệu suất so với các thuật toán khác, nó vẫn có giá trị trong việc giảng dạy và hiểu cơ bản về thuật toán sắp xếp.
Thuật toán sắp xếp nổi bọt cho phép chúng ta khám phá cách hoạt động của một thuật toán sắp xếp cơ bản thông qua việc so sánh và hoán đổi các phần tử. Nó cung cấp một cái nhìn tổng quan về quá trình sắp xếp và khả năng áp dụng các khái niệm cơ bản vào các bài toán thực tế.
Dù không phổ biến trong các ứng dụng thực tế, thuật toán sắp xếp nổi bọt vẫn có ứng dụng trong việc sắp xếp các danh sách nhỏ và trong quá trình giảng dạy lập trình. Việc hiểu và nắm vững cách hoạt động của thuật toán sắp xếp nổi bọt cũng giúp chúng ta dễ dàng tiếp cận và hiểu các thuật toán sắp xếp phức tạp hơn.
Cuối cùng, Bubble Sort không phải là lựa chọn tối ưu cho các dự án lớn và phức tạp, nhưng nó đóng góp vào việc xây dựng nền tảng kiến thức về thuật toán sắp xếp và khám phá cách các thuật toán hoạt động.
Hi vọng các bạn thấy bài viết này hữu ích và hiểu rõ về thuật toán sắp xếp nổi bọt. Nếu có vấn đề gì thì chúng ta cùng nhau bàn luận dưới phần comment nhé! Chúc các bạn thành công.
Tags:
dsa