Khi xử lý dữ liệu, việc sắp xếp là một công việc quan trọng và thường xuyên được thực hiện. Có nhiều thuật toán khác nhau để thực hiện việc sắp xếp, mỗi thuật toán đều có ưu nhược điểm riêng. Trong bài viết này, chúng ta sẽ thảo luận và tìm hiểu về thuật toán sắp xếp chèn - một thuật toán đơn giản và dễ hiểu.
Khái niệm thuật toán sắp xếp chèn
Thuật toán sắp xếp chèn (tiếng Anh: Insertion Sort) là một thuật toán sắp xếp một danh sách dữ liệu theo thứ tự tăng dần hoặc giảm dần bằng cách đưa từng phần tử ở phần chưa được sắp xếp chèn vào vị trí thích hợp tại phần đã được sắp xếp.
Cách thức hoạt động của thuật toán sắp xếp chèn
Để dễ hình dung cách thuật toán hoạt động, các bạn hãy tưởng tượng các bạn có chín mẫu giấy được sắp xếp tăng dần lần lượt đánh số 1, 2, 4, 5, 6, 7, 8, 9, 10 và một mẫu giấy đánh số 3. Các bạn làm thế nào để chèn số 3 đó vào dãy sao cho dãy vẫn giữ nguyên thứ tự của nó? Tất nhiên các bạn sẽ kiểm tra lần lượt từng mẫu giấy từ phải hoặc từ trái sang, khi tìm được vị trí thích hợp rồi các bạn sẽ chèn số 3 vào.
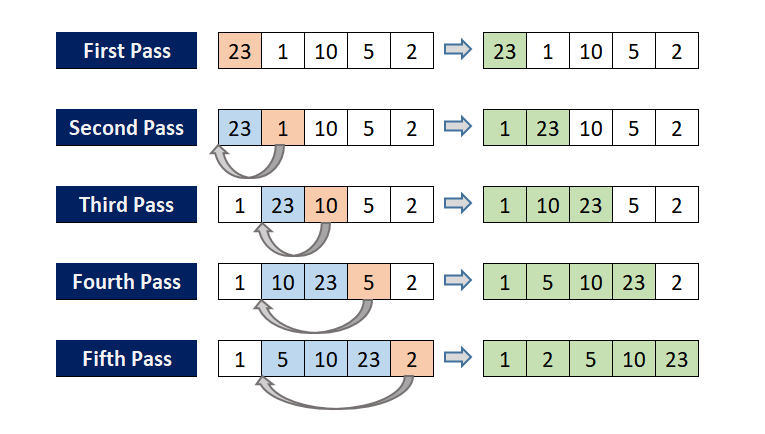
Thuật toán sắp xếp chèn cũng hoạt động tương tự như vậy:
- Bước 1: Giả định phần tử đầu tiên đã được sắp xếp.
- Bước 2: Lấy phần tử tiếp theo trong phần chưa được sắp xếp làm key để chèn, rồi so sánh nó với từng phần tử ở phần đã được sắp xếp.
- Bước 3: Nếu phần tử ở phần đã được sắp xếp lớn hơn key, thì đó chưa phải là vị trí thích hợp để chèn vào. Ta sẽ xê dịch phần tử đó sang bên phải.
- Bước 4: Lặp lại bước 3 cho đến khi tìm được vị trí thích hợp.
- Bước 5: Điền key vào chỗ trống.
- Bước 6: Lặp lại quá trình từ bước 2 cho đến khi tất cả các phần tử đã được đặt vào vị trí đúng.
Giả sử ta có mảng arr = {49, 9, 21, 20, 30, 56, 31} và cần sắp xếp theo thứ tự tăng dần, ta thực hiện như sau:
- Trước hết, ta coi 49 là phần tử đã được sắp xếp. Sau đó ta lấy 9 từ phần chưa được sắp xếp làm key và so sánh với 49. Vì 49 > 9 nên ta xác định vị trí trước 49 sẽ là vị trí thích hợp cho key của chúng ta. Sau đó, ta sẽ dịch chuyển 49 qua bên phải để chừa chỗ rồi chèn key vào.
- Sau đó ta lấy 21 làm key và so sánh với hai phần tử đã được sắp xếp. Ta xác định vị trí nằm giữa hai phần tử 9 và 49 sẽ thích hợp để chèn vào, nên ta tiếp tục dịch chuyển 49 qua phải để tạo chỗ trống và chèn 21 vào.
- Tiếp tục lấy key là 20. Làm tương tự như trên, ta xác định vị trí nằm giữa hai phần tử 9 và 21 phù hợp nên ta sẽ dịch chuyển hai phần tử 21 và 49 qua bên phải rồi chèn key vào.
- Tiếp tục lấy key là 30. Ta xác định vị trí giữa hai phần tử 21 và 49 phù hợp nên ta sẽ dịch chuyển 49 rồi chèn key vào.
- Tiếp tục lấy key là 56. Ta xác định phần tử này đã nằm ở vị trí thích hợp rồi nên ta không cần phải dịch chuyển phần tử nào hết.
- Sau đó lấy 31 làm key. Ta xác định vị trí giữa hai phần tử 30 và 49 phù hợp nên ta sẽ dịch chuyển 49 và 56 rồi sau đó điền key vào chỗ trống.
- Vậy là ta đã hoàn tất sắp xếp mảng bằng thuật toán sắp xếp chèn.
Triển khai thuật toán
Sau đây là cách triển khai thuật toán sắp xếp chèn bằng các ngôn ngữ khác nhau mà bạn có thể tham khảo.
C
#include <stdio.h>// Hàm xuất mảngvoid printArr(int arr[], int arrLength){for (int i = 0; i < arrLength; i++){printf("%d ", arr[i]);}printf("\n");}// Hàm sắp xếpvoid insertionSort(int arr[], int arrLength){// Lặp hết mảng arr. Vì phần tử đầu arr[0] được giả định đã sắp xếp nên bắt đầu tại vị trí ifor (int i = 1; i < arrLength; i++){// arr[i] sẽ nằm ở phần chưa được sắp xếp, chọn phần tử này làm keyint key = arr[i];// Khởi tạo biến j tại vị trí kề trái key để xác định vị trí thích hợp để chèn key vàoint j = i - 1;// Xác định vị trí để chèn, đồng thời dịch chuyển các phần tử trong phần đã sắp xếp sang bên phải// Trong vòng lặp while, khi j < 0 hoặc vị trí tại j bé hơn key là đã xác định vị trí kề phải là vị trí để chèn keywhile (j >= 0 && arr[j] > key){arr[j + 1] = arr[j];j--;}// Đã tìm được vị trí thích hợp, điền key vào chỗ trốngarr[j + 1] = key;}}int main(int argc, char const *argv[]){int arr[] = {49, 9, 21, 20, 30, 56, 31};int arrLength = sizeof(arr) / sizeof(arr[0]);printf("Mang ban dau: ");printArr(arr, arrLength);insertionSort(arr, arrLength);printf("Mang da duoc sap xep: ");printArr(arr, arrLength);return 0;}
C++
#include <iostream>using namespace std;// Hàm xuất mảngvoid printArr(int arr[], int arrLength){for (int i = 0; i < arrLength; i++){cout << arr[i] << " ";}cout << endl;}// Hàm sắp xếpvoid insertionSort(int arr[], int arrLength){// Lặp hết mảng arr. Vì phần tử đầu arr[0] được giả định đã sắp xếp nên bắt đầu tại vị trí ifor (int i = 1; i < arrLength; i++){// arr[i] sẽ nằm ở phần chưa được sắp xếp, chọn phần tử này làm keyint key = arr[i];// Khởi tạo biến j tại vị trí kề trái key để xác định vị trí thích hợp để chèn key vàoint j = i - 1;// Xác định vị trí để chèn, đồng thời dịch chuyển các phần tử trong phần đã sắp xếp sang bên phải// Trong vòng lặp while, khi j < 0 hoặc vị trí tại j bé hơn key là đã xác định vị trí kề phải là vị trí để chèn keywhile (j >= 0 && arr[j] > key){arr[j + 1] = arr[j];j--;}// Đã tìm được vị trí thích hợp, điền key vào chỗ trốngarr[j + 1] = key;}}int main(int argc, char const *argv[]){int arr[] = {49, 9, 21, 20, 30, 56, 31};int arrLength = sizeof(arr) / sizeof(arr[0]);cout << "Mang ban dau: ";printArr(arr, arrLength);insertionSort(arr, arrLength);cout << "Mang da duoc sap xep: ";printArr(arr, arrLength);return 0;}
C#
using System;namespace Main{class Program{// Phương thức xuất mảngstatic void printArr(int[] arr){foreach (int i in arr){Console.Write($"{i} ");}Console.WriteLine();}// Phương thức sắp xếpstatic void insertionSort(int[] arr){// Lặp hết mảng arr. Vì phần tử đầu arr[0] được giả định đã sắp xếp nên bắt đầu tại vị trí ifor (int i = 1; i < arr.Length; i++){// arr[i] sẽ nằm ở phần chưa được sắp xếp, chọn phần tử này làm keyint key = arr[i];// Khởi tạo biến j tại vị trí kề trái key để xác định vị trí thích hợp để chèn key vàoint j = i - 1;// Xác định vị trí để chèn, đồng thời dịch chuyển các phần tử trong phần đã sắp xếp sang bên phải// Trong vòng lặp while, khi j < 0 hoặc vị trí tại j bé hơn key là đã xác định vị trí kề phải là vị trí để chèn keywhile (j >= 0 && arr[j] > key){arr[j + 1] = arr[j];j--;}// Đã tìm được vị trí thích hợp, điền key vào chỗ trốngarr[j + 1] = key;}}static void Main(){int[] arr = {49, 9, 21, 20, 30, 56, 31};Console.Write("Mang ban dau: ");printArr(arr);insertionSort(arr);Console.Write("Mang da duoc sap xep: ");printArr(arr);}}}
Java
import java.util.Arrays;public class Main {// Phương thức sắp xếppublic static void insertionSort(int[] arr) {// Lặp hết mảng arr. Vì phần tử đầu arr[0] được giả định đã sắp xếp nên bắt đầu tại vị trí ifor (int i = 1; i < arr.length; i++) {// arr[i] sẽ nằm ở phần chưa được sắp xếp, chọn phần tử này làm keyint key = arr[i];// Khởi tạo biến j tại vị trí kề trái key để xác định vị trí thích hợp để chèn key vàoint j = i - 1;// Xác định vị trí để chèn, đồng thời dịch chuyển các phần tử trong phần đã sắp xếp sang bên phải// Trong vòng lặp while, khi j < 0 hoặc vị trí tại j bé hơn key là đã xác định vị trí kề phải là vị trí để chèn keywhile (j >= 0 && arr[j] > key) {arr[j + 1] = arr[j];j--;}// Đã tìm được vị trí thích hợp, điền key vào chỗ trốngarr[j + 1] = key;}}public static void main(String[] args) {int[] arr = {49, 9, 21, 20, 30, 56, 31};System.out.println("Mang ban dau: " + Arrays.toString(arr));insertionSort(arr);System.out.println("Mang da duoc sap xep: " + Arrays.toString(arr));}}
Python
# Hàm sắp xếpdef insertionSort(lst):# Lặp hết danh sách. Vì phần tử đầu lst[0] được giả định đã sắp xếp nên bắt đầu tại vị trí ifor i in range(1, len(lst)):# lst[i] sẽ nằm ở phần chưa được sắp xếp, chọn phần tử này làm keykey = lst[i]# Khởi tạo biến j tại vị trí kề trái key để xác định vị trí thích hợp để chèn key vàoj = i - 1# Xác định vị trí để chèn, đồng thời dịch chuyển các phần tử trong phần đã sắp xếp sang bên phải# Trong vòng lặp while, khi j < 0 hoặc vị trí tại j bé hơn key là đã xác định vị trí kề phải là vị trí để chèn keywhile j >= 0 and lst[j] > key:lst[j + 1] = lst[j]j -= 1# Đã tìm được vị trí thích hợp, điền key vào chỗ trốnglst[j + 1] = keylst = [49, 9, 21, 20, 30, 56, 31]print(f"Danh sách ban đầu: {lst}")insertionSort(lst)print(f"Danh sách đã được sắp xếp: {lst}")
JavaScript
// Hàm sắp xếpfunction insertionSort(arr) {// Lặp hết mảng arr. Vì phần tử đầu arr[0] được giả định đã sắp xếp nên bắt đầu tại vị trí ifor (let i = 1; i < arr.length; i++) {// arr[i] sẽ nằm ở phần chưa được sắp xếp, chọn phần tử này làm keylet key = arr[i];// Khởi tạo biến j tại vị trí kề trái key để xác định vị trí thích hợp để chèn key vàolet j = i - 1;// Xác định vị trí để chèn, đồng thời dịch chuyển các phần tử trong phần đã sắp xếp sang bên phải// Trong vòng lặp while, khi j < 0 hoặc vị trí tại j bé hơn key là đã xác định vị trí kề phải là vị trí để chèn keywhile (j >= 0 && arr[j] > key) {arr[j + 1] = arr[j];j--;}// Đã tìm được vị trí thích hợp, điền key vào chỗ trốngarr[j + 1] = key;}}let arr = [49, 9, 21, 20, 30, 56, 31];window.alert("Mảng ban đầu: " + arr);insertionSort(arr);window.alert("Mảng đã được sắp xếp: " + arr);
Phân tích độ phức tạp về thời gian và bộ nhớ
Độ phức tạp về thời gian
Thời gian thực thi của thuật toán sắp xếp chèn phụ thuộc vào số lượng phần tử cần sắp xếp. Độ phức tạp thời gian của thuật toán sắp xếp chèn là O(n2), trong đó n là số lượng phần tử.
Trong quá trình sắp xếp, thuật toán sẽ duyệt qua từng phần tử chưa sắp xếp và so sánh nó với tất cả các phần tử trong phần đã sắp xếp. Vì vậy, số lần so sánh và di chuyển các phần tử sẽ tăng theo bình phương của số lượng phần tử. Khi số lượng phần tử tăng lên, thời gian thực thi sẽ tăng đáng kể và độ phức tạp sẽ là O(n2).
Độ phức tạp về bộ nhớ
Thuật toán sắp xếp chèn không đòi hỏi bộ nhớ phụ để thực hiện thuật toán. Nó chỉ sử dụng một lượng bộ nhớ hằng số để lưu trữ các biến tạm thời và các chỉ số.
Độ phức tạp bộ nhớ của thuật toán sắp xếp chèn là O(1), tức là không phụ thuộc vào số lượng phần tử cần sắp xếp. Kích thước bộ nhớ sử dụng sẽ không thay đổi khi số lượng phần tử tăng lên.
Ưu điểm và hạn chế của thuật toán sắp xếp chèn
Ưu điểm
- Đơn giản và dễ hiểu: Thuật toán sắp xếp chèn có cấu trúc đơn giản và dễ hiểu, rất phù hợp cho việc giảng dạy và học tập cơ bản về thuật toán sắp xếp.
- Hiệu quả với dữ liệu nhỏ: Khi sắp xếp một dãy dữliệu nhỏ, thuật toán sắp xếp chèn cho kết quả tốt với độ phức tạp thấp và hiệu suất cao.
- Không yêu cầu thêm bộ nhớ phụ: Như đã phân tích trên, độ phức tạp về thời gian của sắp xếp chèn là O(1) vì thuật toán không yêu cầu thêm bất kỳ cấu trúc dữ liệu nào và hoàn toàn hoạt động trên chính danh sách nó sắp xếp mà thôi. Điều này giúp tiết kiệm bộ nhớ khi sắp xếp.
Hạn chế
Bên cạnh ưu điểm kể trên, thuật toán sắp xếp chèn có hạn chế không hiệu quả với danh sách lớn. Như đã phân tích trên, thuật toán sắp xếp chèn có độ phức tạp về thời gian là O(n2). Điều này có nghĩa là, giống như các thuật toán cùng độ phức tạp khác, thời gian để thực hiện tăng rất nhanh theo bình phương kích thước danh sách, khiến cho thuật toán trở nên tốn nhiều thời gian.
Ứng dụng
Thuật toán sắp xếp chèn có thể được áp dụng trong các trường hợp sau:
- Sắp xếp các dãy dữ liệu nhỏ: Với các dãy dữ liệu nhỏ, thuật toán sắp xếp chèn cho kết quả tốt và có thể được thực hiện dễ dàng.
- Sắp xếp dữ liệu gần như đã sắp xếp: Khi dữ liệu gần như đã sắp xếp, thuật toán sắp xếp chèn có thể hoạt động hiệu quả hơn các thuật toán khác.
Kết
Trên đây là một cái nhìn tổng quan về thuật toán sắp xếp chèn. Mặc dù có nhược điểm nói trên, thuật toán sắp xếp chèn vẫn là một công cụ hữu ích trong việc sắp xếp dữ liệu đơn giản và nhỏ. Điều quan trọng là qua bài viết này, các bạn đã hiểu và có thể lựa chọn đúng thuật toán phù hợp với tình huống cụ thể để đạt được hiệu suất tốt nhất trong việc xử lý dữ liệu.
Tags:
dsa