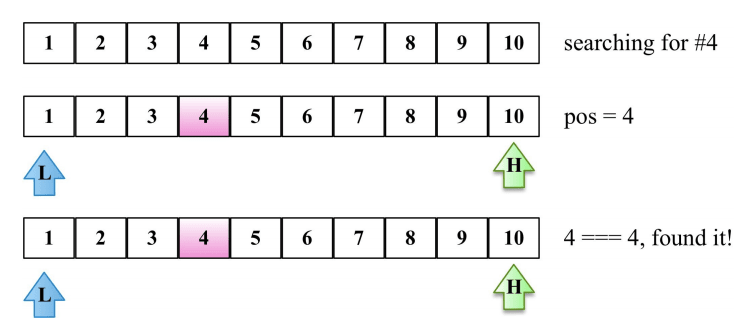
Trong thế giới ngập tràn thông tin, khả năng tìm kiếm nhanh chóng và chính xác là một kỹ năng quan trọng. Trong bài viết này, chúng tôi sẽ giới thiệu về tìm kiếm nội suy - một phương pháp tìm kiếm thông tin mạnh mẽ và hiệu quả. Trong bài viết này, chúng ta sẽ cùng nhau tìm hiểu và thảo luận về khái niệm, cách thức hoạt động, phân tích độ phức tạp, ưu điểm và hạn chế, cũng như ứng dụng của nó.
Khái niệm thuật toán tìm kiếm nội suy
Tìm kiếm nội suy (tiếng Anh: Interpolation Search) là một phương pháp tìm kiếm thông tin trong một tập dữ liệu đã biết, dựa trên các giá trị đã xác định trước. Nó là một sự cải tiến của thuật toán tìm kiếm nhị phân (tìm hiểu tại đây), và có tính linh hoạt hơn so với tìm kiếm nhị phân.
Thuật toán này giúp chúng ta xác định giá trị của một biến dựa trên các giá trị đã biết trong tập dữ liệu. Phương pháp này rất hữu ích khi chúng ta cần tìm giá trị ở giữa các điểm dữ liệu đã biết, mà không cần phải xử lý toàn bộ tập dữ liệu.
Cách thức hoạt động của thuật toán tìm kiếm nội suy
Nói chung, cách hoạt động của thuật toán tìm kiếm nội suy khá tương tự với tìm kiếm nhị phân. Tuy nhiên, thuật toán tìm kiếm nội suy có phần khác biệt. Khác biệt thế nào, chúng ta hãy đào sâu vào phân tích cách thức hoạt động như sau:
- Bước 1: Xác định hai đầu trái phải của phạm vi dò tìm, bắt đầu từ đầu đến cuối tập dữ liệu.
- Bước 2: Xác định điểm dò xét bằng công thức sau:
probe = left + (right - left)(x - array[left]) / (array[right] - array[left])
Trong đó:
- probe: vị trí dò, công thức trên có phép chia nhưng phải lấy phần nguyên
- left: chỉ mục đầu trái của phạm vi
- right: chỉ mục đầu phải của phạm vi
- x: giá trị cần tìm
- array[left]: giá trị đầu trái
- array[right]: giá trị đầu phải
- Bước 3: Nếu giá trị tại vị trí dò nhỏ hơn giá trị cần tìm thì tiếp tục dò bên phải
- Bước 4: Nếu giá trị tại vị trí dò lớn hơn giá trị cần tìm thì tiếp tục dò bên trái
- Bước 5: Nếu giá trị tại vị trí dò đúng bằng giá trị cần tìm thì ngừng dò và kết luận đã tìm thấy phần tử
- Bước 6: Lặp lại các bước trên cho đến khi không còn phạm vi để dò. Nếu hết phạm vi mà không tìm thấy phần tử cần tìm thì kết luận phần tử không tìm thấy.
Triển khai thuật toán
Sau đây là code triển khai thuật toán tìm kiếm nhị phân bằng những ngôn ngữ khác nhau mà bạn có thể tham khảo.
C
#include <stdio.h>// Hàm interpolationSearch() lấy 3 tham sốint interpolationSearch(int arr[], int arrLength, int target){// Khởi tạo phạm vi ban đầuint left = 0;int right = arrLength - 1;while (arr[left] <= target && target <= arr[right] && left <= right){// Xác định điểm thăm dòint probe = left + (right - left) * (target - arr[left]) / (arr[right] - arr[left]);// So sánh arr[probe] với targetif (arr[probe] < target){// Thu hẹp phạm vi về phía bên phảileft = probe + 1;}else if (arr[probe] > target){// Thu hẹp phạm vi về phía bên tráiright = probe - 1;}else{// arr[probe] == target, đã tìm thấy targetreturn probe;}}// Không tìm thấy targetreturn -1;}int main(){int arr[] = {9, 19, 35, 54, 56, 76, 90, 94, 110};// Tính kích thước của mảng arrint arrLength = sizeof(arr) / sizeof(arr[0]);int target = 54;int result = interpolationSearch(arr, arrLength, target);if (result == -1){printf("Phan tu khong tim thay trong mang.");}else{printf("Phan tu tim thay tai vi tri %d.", result);}// Output: 3return 0;}
C++
#include <iostream>using namespace std;// Hàm interpolationSearch() lấy 3 tham sốint interpolationSearch(int arr[], int arrLength, int target){// Khởi tạo phạm vi ban đầuint left = 0;int right = arrLength - 1;while (arr[left] <= target && target <= arr[right] && left <= right){// Xác định điểm thăm dòint probe = left + (right - left) * (target - arr[left]) / (arr[right] - arr[left]);// So sánh arr[probe] với targetif (arr[probe] < target){// Thu hẹp phạm vi về phía bên phảileft = probe + 1;}else if (arr[probe] > target){// Thu hẹp phạm vi về phía bên tráiright = probe - 1;}else{// arr[probe] == target, đã tìm thấy targetreturn probe;}}// Không tìm thấy targetreturn -1;}int main(){int arr[] = {9, 19, 35, 54, 56, 76, 90, 94, 110};// Tính kích thước của mảng arrint arrLength = sizeof(arr) / sizeof(arr[0]);int target = 54;int result = interpolationSearch(arr, arrLength, target);if (result == -1){cout << "Phan tu khong tim thay trong mang.";}else{cout << "Phan tu tim thay tai vi tri " << result;}// Output: 3return 0;}
C#
using System;namespace Main{class Program{// Phương thức interpolationSearch() lấy hai tham sốstatic int interpolationSearch(int[] arr, int target){// Khởi tạo phạm vi ban đầuint left = 0;int right = arr.Length - 1;while (arr[left] <= target && target <= arr[right] && left <= right){// Xác định điểm thăm dòint probe = left + (right - left) * (target - arr[left]) / (arr[right] - arr[left]);// So sánh arr[probe] với targetif (arr[probe] < target){// Thu hẹp phạm vi về phía bên phảileft = probe + 1;}else if (arr[probe] > target){// Thu hẹp phạm vi về phía bên tráiright = probe - 1;}else{// arr[probe] == target, đã tìm thấy targetreturn probe;}}// Không tìm thấy targetreturn -1;}static void Main(string[] args){int[] arr = { 9, 19, 35, 54, 56, 76, 90, 94, 110 };int target = 54;int result = interpolationSearch(arr, target);if (result == -1){Console.WriteLine("Phan tu khong tim thay trong mang.");}else{Console.WriteLine($"Phan tu tim thay tai vi tri {result}.");}// Output: 3}}}
Java
public class Main {// Phương thức interpolationSearch() lấy hai tham sốpublic static int interpolationSearch(int[] arr, int target) {// Khởi tạo phạm vi ban đầuint left = 0;int right = arr.length - 1;while (arr[left] <= target && target <= arr[right] && left <= right) {// Xác định điểm thăm dòint probe = left + (right - left) * (target - arr[left]) / (arr[right] - arr[left]);// So sánh arr[probe] với targetif (arr[probe] < target) {// Thu hẹp phạm vi về phía bên phảileft = probe + 1;} else if (arr[probe] > target) {// Thu hẹp phạm vi về phía bên tráiright = probe - 1;} else {// arr[probe] == target, đã tìm thấy targetreturn probe;}}// Không tìm thấy targetreturn -1;}public static void main(String[] args) {int[] arr = {9, 19, 35, 54, 56, 76, 90, 94, 110};int target = 54;int result = interpolationSearch(arr, target);System.out.println(result == -1? "Phan tu can tim khong co trong mang." : "Tim thay phan tu tai vi tri " + result);// Output: 3}}
Python
# Hàm interpolationSearch() lấy hai tham sốdef interpolationSearch(lst, target):# Khởi tạo phạm vi ban đầuleft = 0right = len(lst) - 1while lst[left] <= target <= lst[right] and left <= right:# Xác định điểm thăm dòprobe = left + (right - left) * (target - lst[left]) // (lst[right] - lst[left])# So sánh lst[probe] với targetif lst[probe] < target:# Thu hẹp phạm vi về phía bên phảileft = probe + 1elif lst[probe] > target:# Thu hẹp phạm vi về phía bên tráiright = probe - 1else:# lst[probe] == target, đã tìm thấy targetreturn probe# Không tìm thấy targetreturn -1lst = [9, 19, 35, 54, 56, 76, 90, 94, 110]target = 54result = interpolationSearch(lst, target)if result == -1:print("Phần tử không tìm thấy trong danh sách")else:print(f"Phần tử tìm thấy tại vị trí {result}")# Output: 3
JavaScript
// Hàm interpolationSearch() lấy hai tham sốfunction interpolationSearch(arr, target) {// Khởi tạo phạm vi ban đầulet left = 0;let right = arr.length - 1;while (arr[left] <= target && target <= arr[right] && left <= right) {// Xác định điểm thăm dòlet probe = Math.floor(left + (right - left) * (target - arr[left]) / (arr[right] - arr[left]));// So sánh arr[probe] với targetif (arr[probe] < target) {// Thu hẹp phạm vi về phía bên phảileft = probe + 1;} else if (arr[probe] > target) {// Thu hẹp phạm vi về phía bên tráiright = probe - 1;} else {// arr[probe] === target, đã tìm thấy targetreturn probe;}}// Không tìm thấy targetreturn -1;}let arr = [9, 19, 35, 54, 56, 76, 90, 94, 110];let target = 54;let result = interpolationSearch(arr, target);if (result === -1) {window.alert("Phần tử không tìm thấy trong mảng.");} else {window.alert("Phần tử tìm thấy tại vị trí " + result);}// Output: 3
Phân tích độ phức tạp về thời gian và bộ nhớ
Độ phức tạp về thời gian
Độ phức tạp về thời gian trung bình của tìm kiếm nội suy là O(log(log n)), trong đó n là số lượng phần tử trong tập dữ liệu. Điều này có nghĩa là thời gian tìm kiếm giảm theo cấp số nhân khi kích thước tập dữ liệu tăng lên. So với tìm kiếm nhị phân, đây là bước cải tiến rất đáng giá. Giải thuật cũng sẽ hiệu quả hơn với những bài toán mà các phần tử trong mảng được phân bố đều.
Độ phức tạp về bộ nhớ
Tìm kiếm nội suy không đòi hỏi nhiều bộ nhớ bổ sung ngoài tập dữ liệu đã biết và một số biến tạm thời. Bộ nhớ cần thiết để lưu trữ dữ liệu trong tìm kiếm nội suy tương đối nhỏ, vì chúng ta chỉ cần lưu trữ các giá trị đã biết trong tập dữ liệu và một số biến tạm thời để tính toán độ dốc và giá trị nội suy. Do đó, độ phức tạp về bộ nhớ của tìm kiếm nội suy được coi là thấp.
Ưu điểm và hạn chế của thuật toán tìm kiếm nội suy
Ưu điểm
Ưu điểm của tìm kiếm nội suy bao gồm:
- Tìm kiếm chính xác: Phương pháp này cho phép chúng ta xác định giá trị chính xác của một biến trong khoảng giữa các điểm dữ liệu đã biết.
- Tốc độ tìm kiếm: Tìm kiếm nội suy thường nhanh hơn so với việc duyệt toàn bộ dữ liệu để tìm kiếm giá trị mong muốn.
Hạn chế
Tuy nhiên, tìm kiếm nội suy cũng có một số hạn chế:
- Giới hạn phạm vi: Tìm kiếm nội suy chỉ hoạt động hiệu quả trong trường hợp giá trị cần tìm nằm trong khoảng giữa hai điểm dữ liệu đã biết. Nếu giá trị cần tìm nằm ngoài phạm vi này, phương pháp này không thể áp dụng.
- Dữ liệu không liên tục: Tìm kiếm nội suy giả định rằng dữ liệu là liên tục và có đặc tính tuyến tính. Trong trường hợp dữ liệu không tuân theo các giả định này, kết quả của tìm kiếm có thể không chính xác.
Ứng dụng
Tìm kiếm nội suy có nhiều ứng dụng trong các lĩnh vực khác nhau. Dưới đây là một số ví dụ:
- Truy vấn dữ liệu: Trong cơ sở dữ liệu, tìm kiếm nội suy có thể được sử dụng để truy vấn thông tin từ các bảng dữ liệu lớn một cách hiệu quả.
- Điều khiển và tự động hóa: Trong các hệ thống điều khiển và tự động hóa, tìm kiếm nội suy có thể được sử dụng để xác định các giá trị trung gian hoặc dự đoán giá trị trong các khung thời gian không cố định.
- Kỹ thuật đồ họa: Trong kỹ thuật đồ họa, tìm kiếm nội suy có thể được sử dụng để tạo ra các hiệu ứng mượt mà và trơn tru trong việc di chuyển và biến đổi đối tượng.
Kết
Tìm kiếm nội suy là một phương pháp tìm kiếm thông tin mạnh mẽ và hiệu quả. Bằng cách sử dụng phương pháp này, chúng ta có thể xác định giá trị chính xác của một biến trong khoảng giữa các điểm dữ liệu đã biết. Mặc dù có một số hạn chế, tìm kiếm nội suy vẫn có nhiều ứng dụng trong các lĩnh vực khác nhau. Hy vọng bài viết này đã giúp bạn hiểu hơn về tìm kiếm nội suy và giá trị của nó trong việc tìm kiếm thông tin.
Tags:
dsa